Set is a collection of different elements. It could be numbers, alphabets, etc. Various symbols are used to denote them (like ℝ denote set of Real Numbers) and their relationship and operation (subset, union, etc).
These set symbols helps to represent mathematical ideas in a concise way and saves space and time. In this blog we have listed all the commonly used Set symbols together and how to get them in Ms Word along with their keyboard shortcuts
List of set symbols along with their meaning and how to get them in Ms Word
Three methods to get symbols in Ms Word
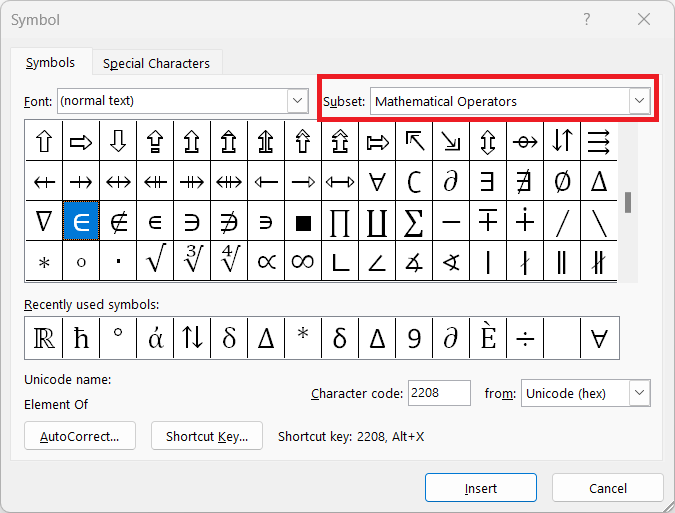
Insert Symbol Method: Go to Insert > Symbols and select More Symbols. In the symbol window, click the desired symbol and hit insert. Following table gives the subset dropdown option of each symbol that can help you find a symbol.
Math AutoCorrect: This is the smartest way to get any symbol in Ms Word. Simply type the Math AutoCorrect text and hit space to get symbol. It works inside Equation editor. However, you can make it work outside equation editor, with following one time setting.
- Go to File > Options to open Word Options
- In Proofing and select AutoCorrect Options
- In Math Autocorrect tab, check box against “Use Math AutoCorrect rules outside of math regions”
Alt X Method: Type the Alt X code of symbol and press Alt + X immediately after it to get symbol.
Let’s say, P = {1, 2, 3, 4} and Q = {1, 3, 5}
| Symbol | Name & Meaning | Example | Subset of Symbol | Math Autocorrect Shortcut (press space after shortcut to get symbol) | Alt X Code (type this code and press Alt+X) |
|---|---|---|---|---|---|
| ℕ | Natural number: All positive integers from 1 till infinity | ℕ = {1, 2, 3, …} | letterlike symbols | \doubleN | 2115 |
| ℤ | Integers: A whole number (not fractional ) that are +ve, -ve or 0 | ℤ = {…, -2, -1,0 ,1 ,2 ,…} | letterlike symbols | \doubleZ | 2124 |
| ℚ | Rational Numbers: a number that is of the form p/q where p and q are integers and q is not equal to 0 | 5, 10.45, 3/7 | letterlike symbols | \doubleQ | 211A |
| 𝔸 | Algebraic numbers: Number that is the solution to a polynomial with rational coefficients | 1, 3/7, √2 | Extended characters – Plane 1 | \doubleA | 1D538 |
| ℝ | Real numbers: A number that includes rational and irrational numbers | 2, π, 2/7 | letterlike symbols | \doubleR | 211D |
| 𝕀 | Imaginary numbers: a real number multiplied by an imaginary unit which is defined by its property i2 = −1 | 5i, πi | Extended characters – Plane 1 | \doubleI | 1D540 |
| ℂ | Complex number: a number of the form a + bi, where a and b are real numbers | 2+3i, 1.5-1i | letterlike symbols | \doubleC | 2102 |
| { } | Set: collection of elements | Q = {1, 3, 5} | – | – | – |
| A ∪ B | Union: in A or B (or both) | P ∪ Q = {1, 2, 3, 4, 5} | Mathematical operators | \bigcup | 222A |
| A ∩ B | Intersection: in both A | P ∩ Q = {1, 3} | Mathematical operators | \bigcap | 2229 |
| A ⊆ B | Subset: every element of A is in B | {1, 3, 5} ⊆ Q or {2, 4} ⊆ P | Mathematical operators | \subseteq | 2286 |
| A ⊂ B | Proper Subset: every element of A is in B, but B has more elements. | Correct: {1, 3} ⊂ Q Incorrect: {1, 3, 5} ⊂ Q | Mathematical operators | \subset | 2282 |
| A ⊄ B | Not a Subset: A is not a subset of B | {5, 6} ⊄ Q | Mathematical Operators | 2284 | |
| A ⊇ B | Superset: A has same elements as B, or more | {1, 3, 5, 7} ⊇ {1, 3, 7} or {1, 3, 5, 7} ⊇ {1, 3, 5, 7} | Mathematical operators | \superseteq | 2287 |
| A ⊃ B | Proper Superset: A has B’s elements and more | Correct: {1, 3, 5, 7} ⊃ {3, 5, 7} Incorrect: {1, 3, 5, 7} ⊃ {1, 3, 5, 7} | Mathematical operators | \superset | 2283 |
| A ⊅ B | Not a Superset: A is not a superset of B | {1, 3, 5, 7} ⊅ {1, 9} | 2285 | ||
| Ac | Complement: Elements not in A | Qc = {1, 2, 6, 7} | – | – | – |
| A − B | Difference: In A but not in B | Let X = {1, 2, 3, 4} and Y = {2, 4}, then X – Y = {1, 3} | – | – | – |
| a ∈ A | Element: a is an element of A | 3 ∈ {1, 2, 3, 4} | Mathematical operator | \in | 2208 |
| b ∉ C | Not an element: b is not an element of C | 2 ∉ {1, 3, 5} | Mathematical operator | \notelement | 2209 |
| Ø | Empty set: { } | {1, 3} ∩ {2, 4} = Ø | Mathematical operator | \emptyset | 2205 |
| 𝕌 | Universal set: the set of all elements or members of all related sets | Extended Characters – Plane 1 | \doubleU | 1D54C | |
| P(A) | Power set: all subset of A | P({a, b}) = { {}, {a}, {b}, {a, b} } | – | – | – |
| A = B | Equality: both sets have the same members | {2, 5, 8} = {8, 2, 5} | – | – | – |
| A×B | Cartesian Product: (set of ordered pairs from A and B) | {1, 2} × {a, b} = {(1, a), (1, b), (2, a), (2, b)} | Latin-1 Supplement | \times | 00D7 |
| |A| | Cardinality: number of elements of set A | |{5, 6}| = 2 | – | – | |
| | | Such that | { n | n > 0 } = {1, 2, 3,…} | – | – | – |
| : | Such that | { n : n > 0 } = {1, 2, 3,…} | – | – | – |
| ∀ | For all | ∀ x >1, x2 > x (for all x greater than 1, x square is greater than x) | Mathematical operators | \forall | 2200 |
| ∃ | There exists | ∃ x | x2 < x (there exists x such that x squared is less than x) | Mathematical operators | \exists | 2203 |
| ∄ | There does not exist | ∄ x | x +1 < x | Mathematical operator | 2204 | |
| ∴ | Therefore | a=b ∴ b=a | Mathematical operators | \therefore | 2234 |

C P Gupta is a YouTuber and Blogger. He is expert in Microsoft Word, Excel and PowerPoint. His YouTube channel @pickupbrain is very popular and has crossed 9.9 Million Views.
Pingback: How to Insert the Intersection Symbol in Word?